Modelling Sympatric speciation

This script aims at reproducing the 1999 article of Doebeli On The Origin of Species By Sympatric Speciation.

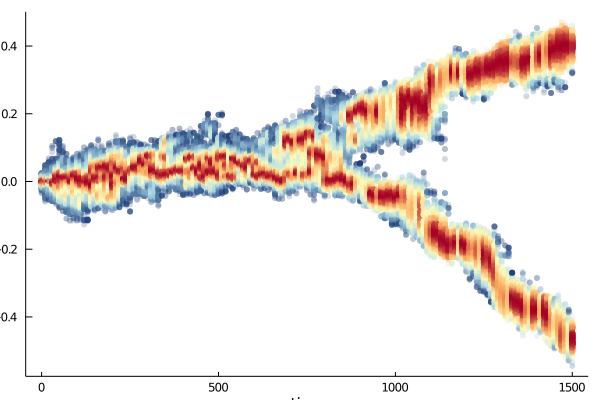
In this article, birth and death functions are defined as gaussian, with respective variance $\sigma_b$ and $\sigma_d$. It is shown that when $\sigma_d < \sigma_b$, speciation in the trait space occurs. This is what we reproduce here.

Running the world

We need to run the simulation for a significant amount of time to observe sympatric speciation. As such, we set ancestors=false. The rest is pretty standard

myspace = (RealSpace{1,Float64}(),)
σ_b = .9;
σ_d = .7;
K0 = 1000
b(X,t) = 1.
d(X,Y,t) = gaussian(X[1],Y[1],σ_d)/K0 / gaussian(X[1],0.,σ_b)
D = (1e-2,)
mu = [.1]
NMax = 2000
tend = 1500
p = Dict{String,Any}();@pack! p = D,mu,NMax
myagents = [Agent(myspace,(1e-2 * randn(),),rates=true) for i in 1:K0]
w0 = World(myagents,myspace,p,0.)
@time sim = run!(w0,Gillepsie(),tend,b,d,dt_saving = 10)
Plots.plot(sim, ylabel = "Adaptive trait")