Inverse ecosystem modeling made easy with PiecewiseInference.jl

Mechanistic ecosystem models permit to quantiatively describe how population, species or communities grow, interact and evolve. Yet calibrating them to fit real-world data is a daunting task. That’s why I’m excited to introduce PiecewiseInference.jl, a new Julia package that provides a user-friendly and efficient framework for inverse ecosystem modeling. In this blog post, I will guide you through the main features of PiecewiseInference.jl and provide a step-by-step tutorial on how to use it with a three-compartment ecosystem model. Whether you’re a quantitative ecologist or a curious data scientist, I hope this post will encourage you to join the effort and use and develop inverse ecosystem modelling methods to improve our understanding and predictions of ecosystems.

Preliminary steps

This tutorial relies on three packages that I have authored but are (yet) not registered on the official Julia registry. Those are

• PiecewiseInference,
• EcoEvoModelZoo: a package which provides access to a collection of ecosystem models,
• ParametricModels: a wrapper package to manipulate dynamical models. Specifically, ParametricModels avoids the hassle of specifying, at each time you want to simulate an ODE model, boring details such as the algorithm to solve it, the time span, etc…

To easily install them on your machine, you’ll have to add my personal registry by doing the following:

using Pkg; Pkg.Registry.add(RegistrySpec(url = "https://github.com/vboussange/VBoussangeRegistry.git"))

Once this is done, let’s import those together with other necessary Julia packages for this tutorial.

using Graphs
using EcoEvoModelZoo
using ParametricModels
using LinearAlgebra
using UnPack
using OrdinaryDiffEq
using Statistics
using SparseArrays
using ComponentArrays
using PythonPlot

We use Graphs to create a directed graph to represent the food web to be considered The OrdinaryDiffEq package provides tools for solving ordinary differential equations, while the LinearAlgebra package is used for linear algebraic computations. The UnPack package provides a convenient way to extract fields from structures, and the ComponentArrays package is used to store and manipulate the model parameters conveniently. Finally, the PythonCall package is used to interface with Python’s Matplotlib library for visualization.

Definition of the forward model

Defining hyperparameters for the forward simulation of the model.

Next, we define the algorithm used for solving the ODE model. We also define the absolute tolerance (abstol) and relative tolerance (reltol) for the solver. tspan is a tuple representing the time range we will simulate the system for, and tsteps is a vector representing the times we want to output the simulated data.

alg = BS3()
abstol = 1e-6
reltol = 1e-6
tspan = (0.0, 600)
tsteps = range(300, tspan[end], length=100)

300.0:3.0303030303030303:600.0

Defining the foodweb structure

We’ll define a 3-compartment ecosystem as presented in McCann et al. (1994). We will use SimpleEcosystemModel from EcoEvoModeZoo.jl, which requires as input a foodweb structure. Let’s use a DiGraph to represent it.

N = 3 # number of compartment

foodweb = DiGraph(N)
add_edge!(foodweb, 2 => 1) # C to R
add_edge!(foodweb, 3 => 2) # P to C

true

The N variable specifies the number of compartments in the model. The add_edge! function is used to add edges to the graph, specifying the flow of resources between compartments.

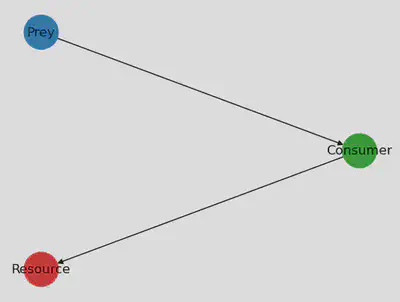
For fun, let’s just plot the foodweb. Here we use the PythonCall and PythonPlot packages to visualize the food web as a directed graph using networkx and numpy. We create a color list for the different species, and then create a directed graph g_nx with networkx using the adjacency matrix of the food web. We also specify the position of each node in the graph, and use nx.draw to draw the graph with

using PythonCall
nx = pyimport("networkx")
np = pyimport("numpy")
species_colors = ["tab:red", "tab:green", "tab:blue"]

g_nx = nx.DiGraph(np.array(adjacency_matrix(foodweb)))
pos = Dict(0 => [0, 0], 1 => [0.2, 1], 2 => [0, 2])
labs = Dict(0 => "Resource", 1 => "Consumer", 2 => "Prey")

fig, ax = subplots(1)
nx.draw(g_nx, pos, ax=ax, node_color=species_colors, node_size=1000, labels=labs)
display(fig)

Defining the ecosystem model

Now that we have defined the foodweb structure, we can build the ecosystem model, which will be a SimpleEcosystemModel from EcoEvoModelZoo.

The next several functions are required by SimpleEcosystemModel and define the specific dynamics of the model. The intinsic_growth_rate function specifies the intrinsic growth rate of each compartment, while the carrying_capacity function specifies the carrying capacity of each compartment. The competition function specifies the competition between and within compartments, while the resource_conversion_efficiency function specifies the efficiency with which resources are converted into consumer biomass. The feeding function specifies the feeding interactions between compartments.

intinsic_growth_rate(p, t) = p.r

function carrying_capacity(p, t)
    @unpack K₁₁ = p
    K = vcat(K₁₁, ones(N - 1))
    return K
end

function competition(u, p, t)
    @unpack A₁₁ = p
    A = spdiagm(vcat(A₁₁, 0, 0))
    return A * u
end

resource_conversion_efficiency(p, t) = ones(N)

resource_conversion_efficiency (generic function with 1 method)

To define the feeding processes, we use adjacency_matrix to get the adjacency matrix of the food web. We then use findnz from SparseArrays to get the row and column indices of the non-zero entries in the adjacency matrix, which we store in I and J. Those are then used to generate sparse matrices required for defining the functional responses of each species considered. The sparse matrices’ non-zero coefficients are the model parameters to be fitted.

using SparseArrays
W = adjacency_matrix(foodweb)
I, J, _ = findnz(W)

([2, 3], [1, 2], [1, 1])

function feeding(u, p, t)
    @unpack H₂₁, H₃₂, q₂₁, q₃₂ = p

    # handling time
    H = sparse(I, J, vcat(H₂₁, H₃₂), N, N)

    # attack rates
    q = sparse(I, J, vcat(q₂₁, q₃₂), N, N)

    return q .* W ./ (one(eltype(u)) .+ q .* H .* (W * u))
end

feeding (generic function with 1 method)

We are done defining the ecological processes.

Defining the ecosystem model parameters for generating a dataset

The parameters for the ecosystem model are defined using a ComponentArray. The u0_true variable specifies the initial conditions for the simulation. The ModelParams type from the ParametricModels package is used to specify the model parameters and simulation settings. Finally, the SimpleEcosystemModel type from the EcoEvoModelZoo package is used to define the ecosystem model.

p_true = ComponentArray(H₂₁=[1.24],
                        H₃₂=[2.5],
                        q₂₁=[4.98],
                        q₃₂=[0.8],
                        r=[1.0, -0.4, -0.08],
                        K₁₁=[1.0],
                        A₁₁=[1.0])

u0_true = [0.77, 0.060, 0.945]

mp = ModelParams(; p=p_true,
    tspan,
    u0=u0_true,
    alg,
    reltol,
    abstol,
    saveat=tsteps,
    verbose=false, # suppresses warnings for maxiters
    maxiters=50_000
)
model = SimpleEcosystemModel(; mp, intinsic_growth_rate,
    carrying_capacity,
    competition,
    resource_conversion_efficiency,
    feeding)

`Model` SimpleEcosystemModel

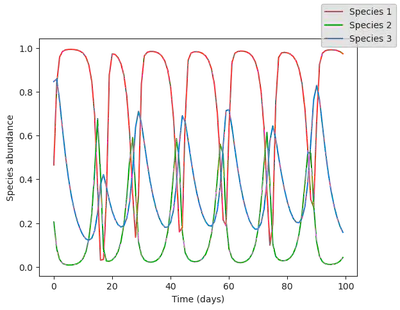
Let’s run the model to generate a dataset! There is nothing more simple than that. Let’s also plot it, to get a sense of what it looks like.

data = simulate(model, u0=u0_true) |> Array

# plotting
using PythonPlot;
function plot_time_series(data)
    fig, ax = subplots()
    for i in 1:N
        ax.plot(data[i, :], label="Species $i", color = species_colors[i])
    end
    # ax.set_yscale("log")
    ax.set_ylabel("Species abundance")
    ax.set_xlabel("Time (days)")
    fig.set_facecolor("None")
    ax.set_facecolor("None")
    fig.legend()
    return fig
end

display(plot_time_series(data))

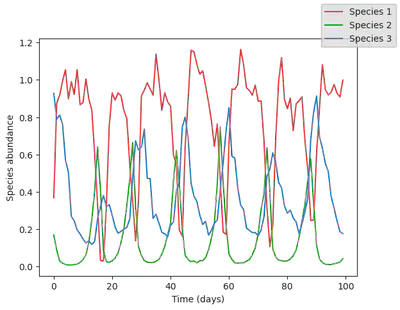
Let’s add a bit of noise to the data to simulate experimental errors. We proceed by adding log normally distributed noise, so that abundance are always positive (negative abundance would not make sense, but could happen when adding normally distributed noise!).

data = data .* exp.(0.1 * randn(size(data)))

display(plot_time_series(data))

Inversion with PiecewiseInference.jl

Now that we have set up our model and generated some data, we can proceed with the inverse modelling using PiecewiseInference.jl.

PiecewiseInference.jl allows to perform inversion based on a segmentation method that partitions the data into short time series (segments), each treated independently and matched against simulations of the model considered. The segmentation approach helps to avoid the ill-behaved loss functions that arise from the strong nonlinearities of ecosystem models, when formulation the inference problem. Note that during the inversion, not only the parameters are inferred, but also the initial conditions, which are necessary to simulate the ODE model.

Definition of the InferenceProblem

We first import the packages required for the inversion. PiecewiseInference is the main package used, but we also need OptimizationFlux for the Adam optimizer, and SciMLSensitivity to define the sensitivity method used to differentiate the forward model.

using PiecewiseInference
using OptimizationFlux
using SciMLSensitivity

To initialize the inversion, we set the initial values for the parameters in p_init to those of p_true but modify the H₂₁ parameter.

p_init = p_true
p_init.H₂₁ .= 2.0 #

1-element view(::Vector{Float64}, 1:1) with eltype Float64:
 2.0

Next, we define a loss function loss_likelihood that compares the observed data with the predicted data. Here, we use a simple mean-squared error loss function while log transforming the abundance, since the noise is log-normally distributed.

loss_likelihood(data, pred, rg) = sum((log.(data) .- log.(pred)) .^ 2)# loss_fn_lognormal_distrib(data, pred, noise_distrib)

loss_likelihood (generic function with 1 method)

We then define the InferenceProblem, which contains the forward model, the initial parameter values, and the loss function.

infprob = InferenceProblem(model, p_init; loss_likelihood);

It is also handy to use a callback function, that will be called after each iteration of the optimization routine, for visualizing the progress of the inference. Here, we use it to track the loss value and plot the data against the model predictions.

info_per_its = 50
include("cb.jl") # defines the `plotting_fit` function
function callback(p_trained, losses, pred, ranges)
    if length(losses) % info_per_its == 0
        plotting_fit(losses, pred, ranges, data, tsteps)
    end
end

callback (generic function with 1 method)

piecewise_MLE hyperparameters

To use piecewise_MLE, the main function of PiecewiseInference to estimate the parameters that fit the observed data, we need to decide on two critical hyperparameters

• group_size: the number of data points that define an interval, or segment. This number is usually small, but should be decided upon the dynamics of the model: to more nonlinear is the model, the lower group_size should be. We set it here to 11
• batch_size: the number of intervals, or segments, to consider on a single epoch. The higher the batch_size, the more computationally expensive a single iteration of piecewise_MLE, but the faster the convergence. Here, we set it to 5, but could increase it to 10, which is the total number of segments that we have.

Another critical parameter to be decided upon is the automatic differentiation backend used to differentiate the ODE model. Two are supported, Optimization.AutoForwardDiff() and Optimization.Autozygote(). Simply put, Optimization.AutoForwardDiff() is used for forward mode sensitivity analysis, while Optimization.Autozygote() is used for backward mode sensitivity analysis. For more information on those, please refer to the documentation of Optimization.jl.

Other parameters required by piecewise_MLE are

• optimizers specifies the optimization algorithm to be used for each batch. We use the Adam optimizer, which is the go-to optimizer to train deep learning models. It has a learning rate parameter that controls the step size at each iteration. We have chosen a value of 1e-2 because it provides good convergence without causing numerical instability,

• epochs specifies the number of epochs to be used for each batch. We chose a value of 500 because it is sufficient to achieve good convergence,

• info_per_its specifies after how many iterations the callback function should be called

• verbose_loss prints the value of the loss function during training,

@time res = piecewise_MLE(infprob;
                        adtype = Optimization.AutoZygote(),
                        group_size = 11,
                        batchsizes = [5],
                        data = data,
                        tsteps = tsteps,
                        optimizers = [Adam(1e-2)],
                        epochs = [500],
                        verbose_loss = true,
                        info_per_its = info_per_its,
                        multi_threading = false,
                        cb = callback)

piecewise_MLE with 100 points and 10 groups.
Current loss after 50 iterations: 36.745952018526495
Current loss after 100 iterations: 15.064711239454626
Current loss after 150 iterations: 9.993029255013324
Current loss after 200 iterations: 7.994491307947515
Current loss after 250 iterations: 6.500818892986831
Current loss after 300 iterations: 5.3892647156988565
Current loss after 350 iterations: 3.0351181646280514
Current loss after 400 iterations: 2.674445730720996
Current loss after 450 iterations: 3.1591980829795676
Current loss after 500 iterations: 2.4343376293865995
157.765049 seconds (1.70 G allocations: 154.827 GiB, 10.16% gc time, 31.31%
 compilation time: 1% of which was recompilation)
`InferenceResult` with model SimpleEcosystemModel

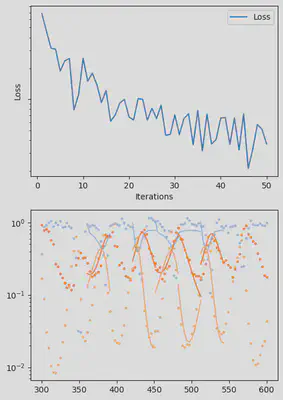
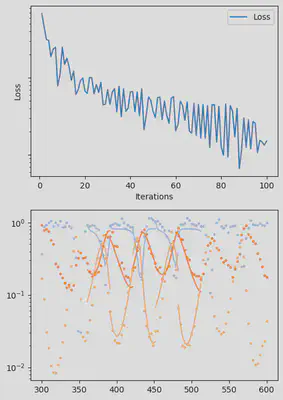
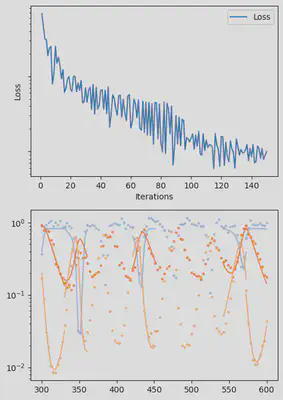
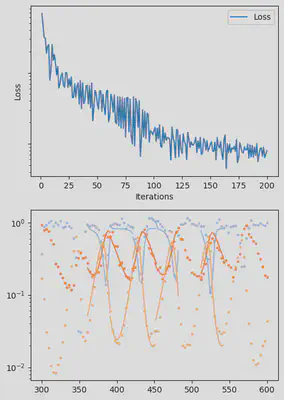
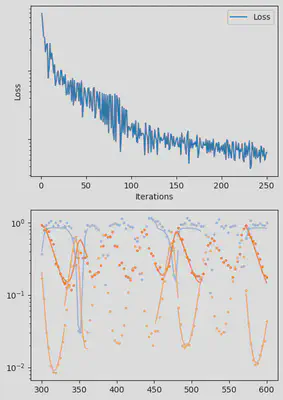
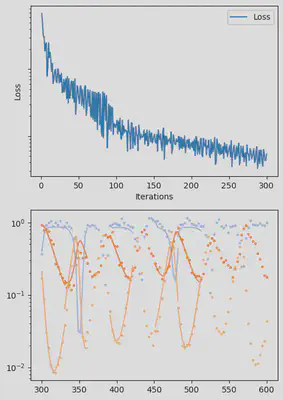
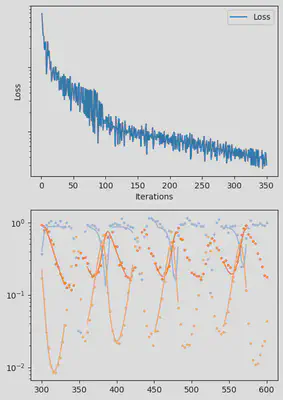
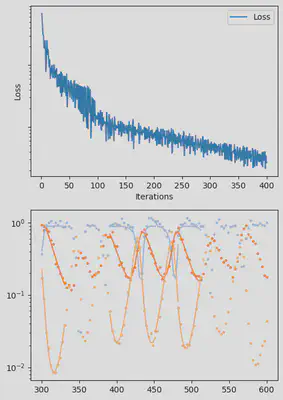
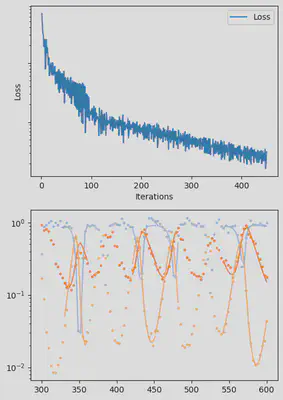
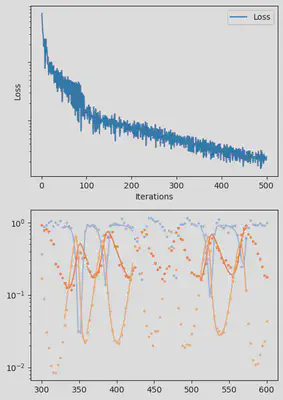
Finally, we can examine the results of the inversion. We can look at the final parameters, and the initial conditions inferred for each segement:

# Some more code
p_trained = res.p_trained
u0s_trained = res.u0s_trained

function print_param_values(p_trained, p_true)
    for k in keys(p_trained)
        println(string(k))
        println("trained value = "); display(p_trained[k])
        println("true value ="); display(p_true[k])
    end
end

print_param_values(p_trained, p_true)

H₂₁
trained value = 
1-element Vector{Float64}:
 1.4786844814887716
true value =
1-element Vector{Float64}:
 2.0
H₃₂
trained value = 
1-element Vector{Float64}:
 1.891238277791975
true value =
1-element Vector{Float64}:
 2.5
q₂₁
trained value = 
1-element Vector{Float64}:
 4.550896291686214
true value =
1-element Vector{Float64}:
 4.98
q₃₂
trained value = 
1-element Vector{Float64}:
 0.7250599871665505
true value =
1-element Vector{Float64}:
 0.8
r
trained value = 
3-element Vector{Float64}:
  0.8705446490535288
 -0.30124597815843823
 -0.08241879418666838
true value =
3-element Vector{Float64}:
  1.0
 -0.4
 -0.08
K₁₁
trained value = 
1-element Vector{Float64}:
 1.0397189294700315
true value =
1-element Vector{Float64}:
 1.0
A₁₁
trained value = 
1-element Vector{Float64}:
 0.972947353012839
true value =
1-element Vector{Float64}:
 1.0

Your turn to play!

You can try to change e.g. the batch_sizes and the group_size. How do those parameters influence the quality of the inversion?

Conclusion

PiecewiseInference.jl provides an efficient and flexible way to perform inference on complex ecological models, making use of automatic differentiation and optimizers traditionally used in Machine Learning. The segmentation method implemented in PiecewiseInference.jl regularizes the inference problem and enables inverse modelling of complex dynamical systems, for which standard methods would otherwise fail.

Furthermore, PiecewiseInference.jl together with EcoEvoModelZoo.jl offer a powerful toolkit for ecologists and evolutionary biologists to benchmark and validate models against data. The combination of theoretical modelling and data can provide new insights into complex ecological systems, helping us to better understand and predict the dynamics of biodiversity.

We invite users to explore these packages and contribute to their development, by adding new models to the EcoEvoModelZoo.jl and improve the features of PiecewiseInference.jl. With these tools, we can continue to push the boundaries of ecological modelling and make important strides towards a more sustainable future.

Appendix

You can find the corresponding tutorial as a .jmd file at https://github.com/vboussange/MyTutorials. Please contact me, if you have found a mistake, or if you have any comment or suggestion on how to improve this tutorial.