Victor Boussange

Victor Boussange

Postdoctoral researcher

WSL Birmensdorf

ETH Zürich

Biography

Greeting! I’m Victor, a postdoctoral researcher in the Dynamic Macroecology Group at the Swiss Federal Institute for Forest, Snow & Landscape (WSL), Switzerland.

My work is centered on developing innovative models and methods to better understand and forecast the dynamics of ecosystems. With the objective of providing a more refined quantitative understanding of ecosystems and enhancing our ability to forecast their responses to disruptions, my focus lies at the interface between process-based ecosystem modeling and machine learning. I specifically attempt to leverage the potential extrapolation ability of theoretically grounded model with the flexibility of state-of-the-art data driven techniques.

Besides work, I am passionate about outdoor adventures and spend my freetime climbing and descending mountains 🏔 , be it with chalk, ice-axes, skis, or a mountainbike. I also enjoy sailing and surfing from time to time. You can check out my alpine CV here.

Interests
  • Ecology and evolution
  • Mathematical modeling
  • Scientific machine learning
  • Complex systems
Education

  • PhD in Environmental Sciences, 2022

    ETH Zürich, Switzerland

  • MSc in Energy and Environmental Sciences, 2018

    INSA Lyon, France

Research projects 🔬

Click on each project to learn more.

*
All Scientific Machine Learning Ecology and evolution Economics
Ecology informed machine learning
In order to anticipate the responses of ecosystems to anthropogenic pressure and climate change, models that can extrapolate ecological dynamics beyond observations are required. While we know very well the laws of physics, we are very far from a predictive theory of life. Machine learning can help filling this huge gap! 🧠 🤖 🌱
Ecology informed machine learning
Econobiology: What can economics learn from biology?
Economic actors develop competitive and mutualistic interactions and evolve through time, in similar ways as groups of species. I rely on scientific machine learning to understand how evolutionary processes arising in economic systems connect to those observed in biological systems.
Econobiology: What can economics learn from biology?
Machine learning to solve highly dimensional non-local nonlinear PDEs
Partial Differential Equations (PDEs) are equations that arise in a variety of models in physics, engineering, finance and biology. I develop numerical schemes based on machine learning techniques to solve for a special class of PDEs (cf below) in high dimension.
Machine learning to solve highly dimensional non-local nonlinear PDEs
Gaining a mechanistic understanding of spatial biodiversity patterns
Biodiversity results from differentiation mechanisms developing within biological populations. Such mechanisms are influenced by the properties of the landscape over which individuals interact, disperse and evolve. The documentation of high levels of species diversity in complex mountain region or riverine systems suggest that some peculiar landscape properties foster diversity. I use mathematical models to investigate how landscape connectivity and habitat heterogeneity foster diversity.
Gaining a mechanistic understanding of spatial biodiversity patterns

Open source softwares 🧑🏽‍💻

Open source as a philosphy.

EvoId.jl

Evolutionary Individual based modelling, mathematically grounded. A user friendly package aimed at simulating the evolutionary dynamics of a population structured over a complex spatio-evolutionary structures.

Star

HighDimPDE.jl

Solver for highly dimensional, non-local, nonlinear PDEs. It is integrated within the SciML ecosystem (see below). Try it out! 😃 If you want to learn more about the algorithms implemented, check out my research interests.

Star

PiecewiseInference.jl

Suite for parameter inference and model selection with dynamical models characterised by complex dynamics.

Star

ParametricModels.jl

Utilities for parametric and composite differential equation models.

Star

EcoEvoModelZoo.jl

A zoo of eco-evolutionary models with high fitness.

Star

SciML

I am a member of the SciML organisation, an open source ecosystem for Scientific Machine Learning in the Julia programming language. On top of being the main author of HighDimPDE.jl, I actively participate in the development of other packages such as DiffEqFlux.jl, a library to train differential equations with data.

Star


I am also a reviewer at the Journal of Open Source Software Science (JOSS).

Featured Publications

Alexander Skeels, Lydian Boschman, Ian R. McFadden, Elizabeth Marie Joyce, Oskar Hagen, Octavio Jiménez Robles, Wilhelmine Bach, Victor Boussange, Thomas Keggin, Walter Jetz, Loïc Pellissier
July, 2023 Science
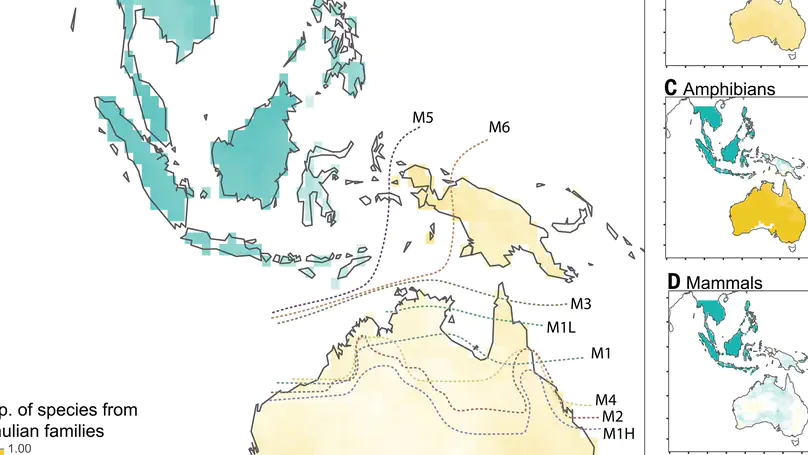
Paleoenvironments shaped the exchange of terrestrial vertebrates across Wallace’s Line
Paleoenvironments shaped the exchange of terrestrial vertebrates across Wallace’s Line

Faunal turnover in Indo-Australia across Wallace’s Line is one of the most recognizable patterns in biogeography and has catalyzed debate about the role of evolutionary and geoclimatic history in biotic interchanges. Here, analysis of more than 20,000 vertebrate species with a model of geoclimate and biological diversification shows that broad precipitation tolerance and dispersal ability were key for exchange across the deep-time precipitation gradient spanning the region. Sundanian (Southeast Asian) lineages evolved in a climate similar to the humid “stepping stones” of Wallacea, facilitating colonization of the Sahulian (Australian) continental shelf. By contrast, Sahulian lineages predominantly evolved in drier conditions, hampering establishment in Sunda and shaping faunal distinctiveness. We demonstrate how the history of adaptation to past environmental conditions shapes asymmetrical colonization and global biogeographic structure.
PDF Cite Project DOI
Victor Boussange, Didier Sornette, Heike Lischke, Loïc Pellissier
January, 2023 arRxiv
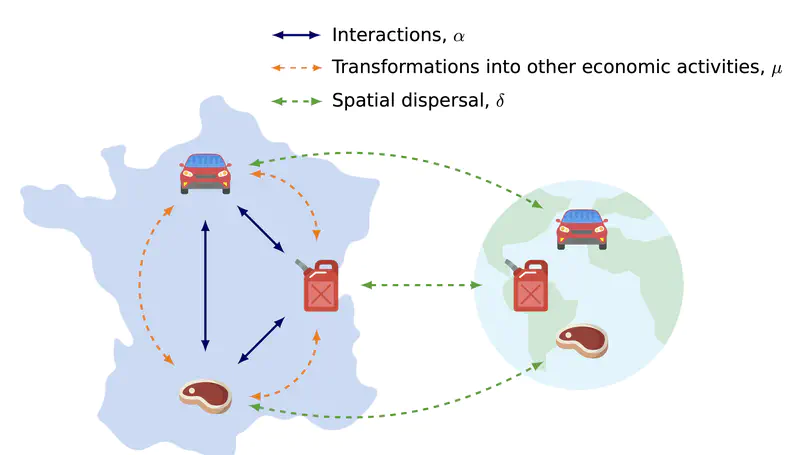
Processes analogous to ecological interactions and dispersal shape the dynamics of economic activities
Processes analogous to ecological interactions and dispersal shape the dynamics of economic activities

Analogies between organisational routines and genes, firms and phenotypes, economic activities and biological populations, and between the processes acting upon these entities, have been used to advance our qualitative understanding of mechanisms driving economic change. Yet, it remained unclear whether biological concepts can be used to quantitatively describe long-term economic change. Here, we use an inverse modelling framework together with economic time-series data to test whether eco-evolutionary processes can explain the collective dynamics of national economic activities. Comparing the support of different biologically inspired dynamic community models against a null model, we find evidence for positive interactions between economic activities and their spatial dispersal.
PDF Cite Code Project DOI
See all publications

Recent Posts

Open source navigation system for sailing
Back in the days, people used to orient themselves with paper maps and the stars or with a sextant. Unfortunately, we have lost this knowledge. It would now be difficult, at least for me, to live without a digital map and a GPS.
Victor Boussange
May 26, 2023 6 min read Sailing tutorials
Open source navigation system for sailing
On combining machine learning-based and theoretical ecosystem models
In this post, I explore the benefits and drawbacks of using empirical (ML)-based models versus mechanistic models for predicting ecosystem responses to perturbations, and further develeop a hybrid approach combining their strengths.
Victor Boussange
Mar 31, 2023 14 min read
Inverse ecosystem modeling made easy with PiecewiseInference.jl
This blog post discusses the use of PiecewiseInference.jl, a Julia package that enables the use of machine learning to fit complex ecological models on ecological dataset.
Mar 26, 2023 11 min read
A practical introduction to approximate Bayesian computation
In this tutorial, you’ll learn the basics of approximate Bayesian computation (ABC). ABC is an inference method with very little requirements in terms of the model structure - yet it can be very powerful. It is very simple to apply to any model, and to understand. We’ll play around with Julia, and we will visualize graphically the inference results, so that you can build an intuition of the inference method.
Nov 27, 2022 10 min read
Create and deploy your Hugo website
This website is based on the wowchemy template that relies on Hugo, a fast framework for building static websites. Although Hugo has many advantages over its brother Jekyll, a Hugo website is not as easy to deploy on GitHub Pages, the free service offered by GitHub to host a personal website.
Mar 27, 2022 3 min read
See all posts

Publications & Talks

Publications

  • Alsos, I.G., Boussange, V., Rijal, D.P., Beaulieu, M., Brown, A.G., Herzschuh, U., Svenning, J.C., Pellissier, L., Ancient sedimentary DNA to forecast trajectories of ecosystem under climate change. (2023). Accepted in Philosophical Transactions of the Royal Society B. [preprint]

  • Skeels, A., Boschman, L. M., McFadden, I. R., Joyce, E.M., Hagen, O., Jiménez Robles, O., Bach, W., Boussange, V., Keggin, T., Jetz, W., Pellissier, L., Paleoenvironments shaped the exchange of terrestrial vertebrates across Wallace’s Line. Science 381, 86-92 (2023).

  • Boussange, V., Becker, S., Jentzen, A., Kuckuck, B., Pellissier, L., Deep learning approximations for non-local nonlinear PDEs with Neumann boundary conditions. Partial Differ. Equ. Appl. 4 (2022), Paper no. 51, 59 pp. [arXiv]

  • Boussange, V. & Pellissier, L., Eco-evolutionary model on spatial graphs reveals how habitat structure affects phenotypic differentiation. Commun Biol 5, 668 (2022). [bioRxiv]

Preprints

  • Boussange, V., Sornette, D., Lischke, H., Pellissier, L., Processes analogous to ecological interactions and dispersal shape the dynamics of economic activities. [arXiv] (2023), 23 pages. In review.

  • Boussange, V., Vilimelis-Aceituno, P., Pellissier, L., Mini-batching ecological data to improve ecosystem models with machine learning. [bioRxiv] (2022), 46 pages. In review.

Proceedings

  • Poulet, T., Alevizos, S., Veveakis, M., Boussange, V., Regenauer-Lieb, K., Episodic mineralising fluid injection through chemical shear zones. ASEG Extended Abstracts (2018), 5 pages.

Monographs

  • Boussange, V., Forward and inverse modelling of eco-evolutionary dynamics in ecological and economic systems. [ETH library] (2022), 207 pages.

Other resources

Works in progress

  • Boussange, V., Karger, D., Malle, J. T., Midolo, D., Unveiling climate-biodiversity interactions: linking earth system and biodiversity models. (in alphabetical order)

Talks

  • Introduction to Julia for Geosciences, co-convener, Short course at EGU 2024, Vienna, Austria (April 2024)
  • A scalable machine learning approach to assess the combined effect of habitat loss and climate change on biodiversity, speaker, International Biogeography Society conference 2024, Prague, Czech Republic (January 2024).
  • Learning from scarce data by combining machine learning and fundamental ecological knowledge, invited speaker, Bioinformatics seminar, Fribourg University, Fribourg, Switzerland (December 2023). [slides]
  • PiecewiseInference.jl: a machine learning framework for inverse ecosystem modelling, speaker, EGU 2023, Vienna, Austria (April 2023). [slides]
  • Combining eco-evolutionary theory and machine learning to advance our understanding of living systems, invited speaker, Seminar at the Laboratoire interdisciplinaire de physique (LiPhy), Grenoble, France (February 2023). [slides]
  • HighDimPDE.jl: A Julia package for solving high-dimensional PDEs, JuliaCon2022, online video 📺
  • Interpretable machine learning for forecasting dynamical processes in ecosystems, World Biodiversity Forum, Davos, Switzerland (June 2022). [slides]
  • Investigating empirical patterns of biodiversity with mechanistic eco-evolutionary models, invited speaker, Seminar at the Theoretical Ecology and Evolution group, Universität Bern (June 2022).
  • Deep learning approximations for non-local nonlinear PDEs, invited speaker, StAMBio seminar, St Andrews, UK (November 2021).
  • Graph topology and habitat assortativity drive phenotypic differentiation in an eco-evolutionary model, Conference on Complex Systems, Lyon, France (October 2021). [slides]
  • Using graph-based metrics to assess the effect of landscape topography on diversification, ECBC, Amsterdam, Netherlands (October 2021). [slides]
  • Solving non-local nonlinear Partial Differential Equations in high dimensions with HighDimPDE.jl, International Conference on Computational Methods in Systems Biology, Bordeaux, France (October 2021). [poster]
  • Responses of neutral and adaptive diversity to complex geographic population structure, Mathematical Population Dynamics, Ecology and Evolution, CIRM Marseille, France (April 2021). [poster]

Popular Topics

Applied Mathematics Biodiversity Biogeography Deep Learning Eco-evolutionary dynamics Ecology and evolution Economic complexity economic system Economics Ecosystem modelling Evolutionary ecology Food-webs Inverse modelling Julia Mathematical modelling Model selection Network topology PDEs Population dynamics Scientific Machine Learning