Machine learning to solve highly dimensional non-local nonlinear PDEs
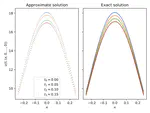
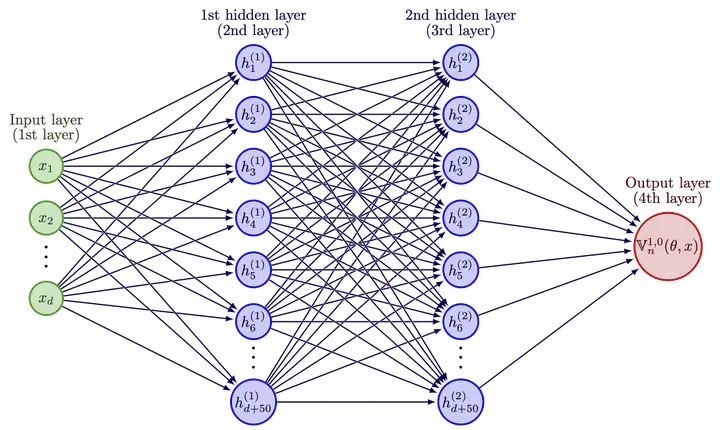 Neural network architectures used to approximate solutions to Eq. (1). The output neuron $\mathbb{V}_n(\theta ,x)$ approximates $u(t_n,x)$.
Neural network architectures used to approximate solutions to Eq. (1). The output neuron $\mathbb{V}_n(\theta ,x)$ approximates $u(t_n,x)$.
Partial Differential Equations (PDEs) are equations that arise in a variety of models in physics, engineering, finance and biology. I develop numerical methods based on machine learning techniques to simulate a special class of PDEs in high dimension, that can capture non-locality (cf generic form of the PDEs below). Such PDEs permit to e.g. model the evolution of biological populations in a realistic manner, by describing the dynamics of several traits characterising individuals. For plants, traits correspond for instance to flower colour, specific leaf area, seed mass, etc…. These characteristics define a high dimensional space that must be considered when modelling ecological and evolutionary processes in biological populations, as they determine the overall fitness of a population in a given environment.
](/media/misc/hemerocallis_hu5a7d427b548baca5d48d20c73022fb53_88058_99dfd9ed3505ee79f64ac6a84682cfb0.webp)
High dimensionality leads to numerical difficulties in simulating the models. The methods I develop overcome this so-called “curse of dimensionality”.
The equation below defines the class of PDEs I am interested in. These PDEs are also referred in the literature as non-local reaction diffusion equations.
$$ \begin{aligned} (\tfrac{\partial}{\partial t}u)(t,x) &= \int_{D} f\big(t,x,{\bf x}, u(t,x),u(t,{\bf x}), ( \nabla_x u )(t,x ),( \nabla_x u )(t,{\bf x} ) \big) \, \nu_x(d{\bf x}) \\ & \quad + \big\langle \mu(t,x), ( \nabla_x u )( t,x ) \big\rangle + \tfrac{ 1 }{ 2 } \text{Trace}\big( \sigma(t,x) [ \sigma(t,x) ]^* ( \text{Hess}_x u)( t,x ) \big). \end{aligned} $$
I have implemented those schemes in HighDimPDE.jl, a Julia package that should allow scientists to develop models that better capture the complexity of life. These techniques extend beyond biology and are also relevant for other fields, such as finance.