Deep learning approximations for non-local nonlinear PDEs with Neumann boundary conditions
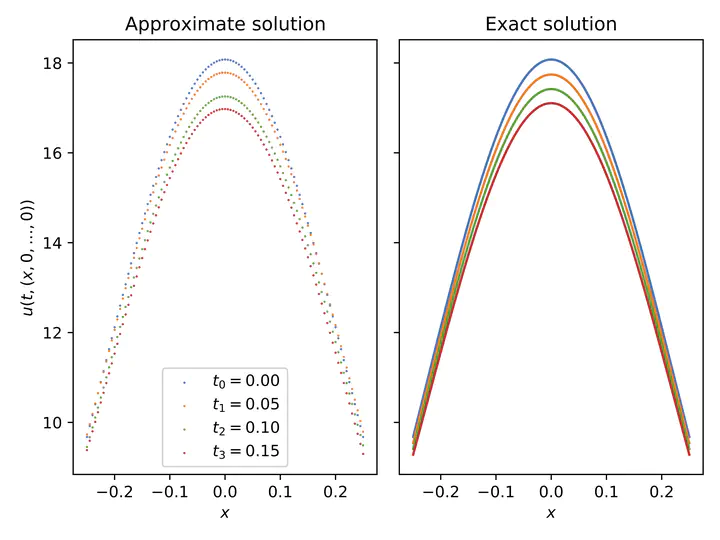 Plot of a machine learning-based approximation of the solution of a replicator-mutator PDE in dimension 5.
Plot of a machine learning-based approximation of the solution of a replicator-mutator PDE in dimension 5.
Abstract
Nonlinear partial differential equations (PDEs) are used to model dynamical processes in a large number of scientific fields, ranging from finance to biology. In many applications standard local models are not sufficient to accurately account for certain non-local phenomena such as, e.g., interactions at a distance. In order to properly capture these phenomena non-local nonlinear PDE models are frequently employed in the literature. In this article we propose two numerical methods based on machine learning and on Picard iterations, respectively, to approximately solve non-local nonlinear PDEs. The proposed machine learning-based method is an extended variant of a deep learning-based splitting-up type approximation method previously introduced in the literature and utilizes neural networks to provide approximate solutions on a subset of the spatial domain of the solution. The Picard iterations-based method is an extended variant of the so-called full history recursive multilevel Picard approximation scheme previously introduced in the literature and provides an approximate solution for a single point of the domain. Both methods are mesh-free and allow non-local nonlinear PDEs with Neumann boundary conditions to be solved in high dimensions. In the two methods, the numerical difficulties arising due to the dimensionality of the PDEs are avoided by (i) using the correspondence between the expected trajectory of reflected stochastic processes and the solution of PDEs (given by the Feynman-Kac formula) and by (ii) using a plain vanilla Monte Carlo integration to handle the non-local term. We evaluate the performance of the two methods on five different PDEs arising in physics and biology. In all cases, the methods yield good results in up to 10 dimensions with short run times. Our work extends recently developed methods to overcome the curse of dimensionality in solving PDEs.